Sampling transforms
Last updated: Apr 24, 2021
Summary
We want to output the most likely program given a natural language utterance and a dataset of past interactions.
Instead of solving the general problem, we will propose a sampling heuristic that approximates our desired output. Specifically, we
Obtain a dense representation of programs.
Sample programs that are likely according to our current dataset. This includes programs in the dataset labeled with utterances similar to the input utterance, as well as transforms in the “local neighborhood” of those transforms in the dataset.
We present two local sampling strategies. A simple “most similar \(k\) out of \(n\)” scheme and a grammar-based sampling strategy guided by a neural network.
Algorithm
We want to rank the infinite set \(T = \{t_1, t_2, \ldots\}\) of transformations according to
\[P(t| u, D) \propto \sum_{t'} \sum_{u'} \operatorname{sim}(u, u') \mathbb{1}_{t' \in D[u']} P(t | t')\]
where \(u\) is a natural language utterance, \(D\) is a dataset of labeled transforms (i.e. \(D\) is a mapping \(u \to \{t_i\}\)) and \(\operatorname{sim}(u, u')\) is computed using a word2vec embedding.
Instead of ranking the entire set and because we have an incomplete dataset \(D'\), we instead sample transformations that are very likely according to the current dataset \(D'\). Specifically, given an utterance \(u\) and the current dataset \(D'\), to sample a list of transforms that have a high value of \(P(t| u, D)\) we
Take the \(k\) most similar utterances \(\{u'_i\}_{i=1}^{i=k} \subseteq D'\) to \(u\) (i.e. with the highest \(\operatorname{sim}(u, u')\)).
Add to the output list the transforms \(t'\) in the dataset that are labeled with any of the \(u'_i\) (because they have \(\mathbb{1}_{t' \in D'[u'_i]} = 1\) and high \(P(t|t'))\).
For each of the transforms \(t'\) added in the previous step sample \(k_2\) transforms \(t''\) that are semantically similar (we assume that such transforms have \(\mathbb{1}_{t' \in D[u'_i]}=1\) in the complete dataset).
Return the list with all the sampled transforms.
The algorithm is summarized below:
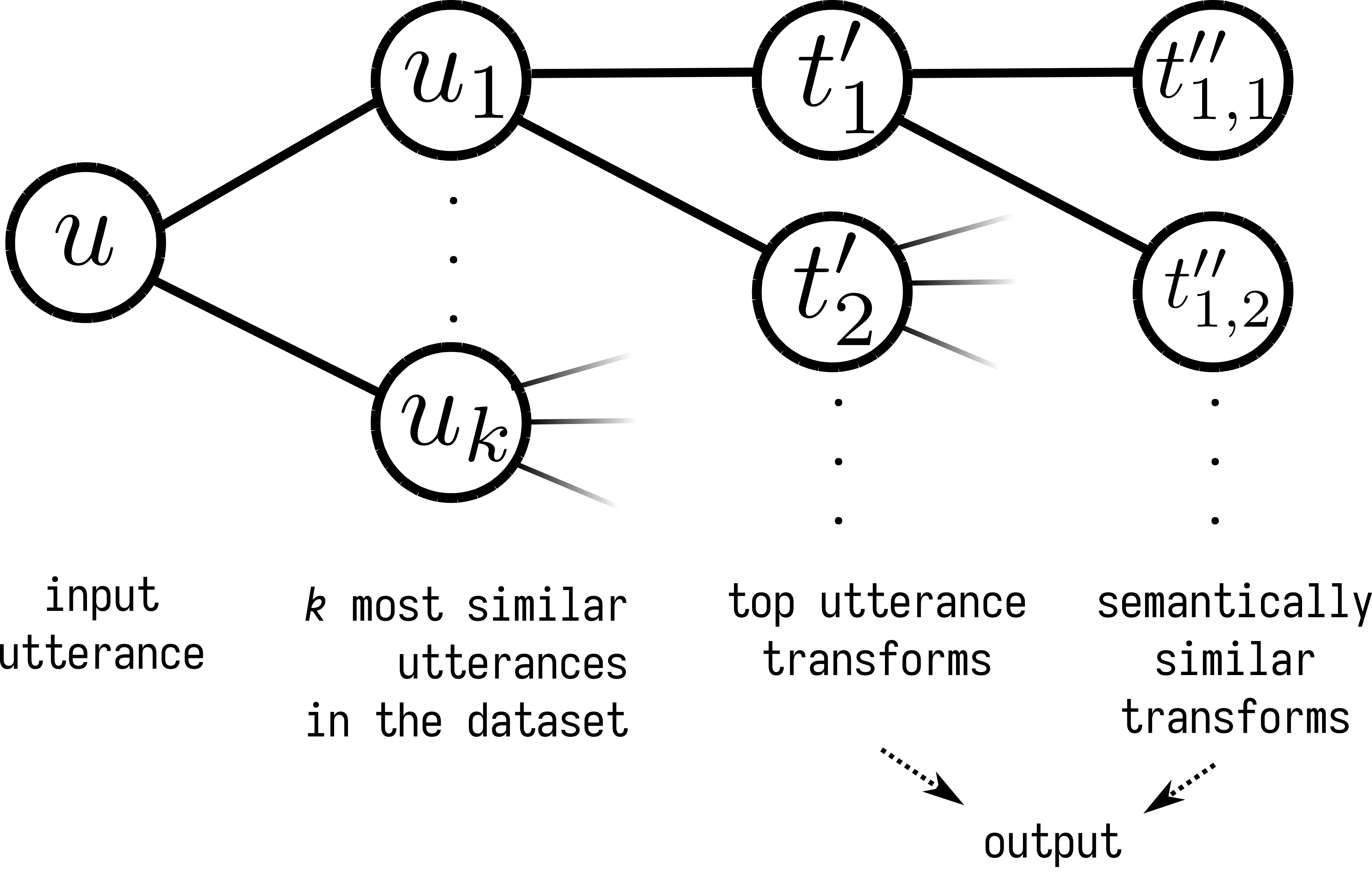
Sampling algorithm.
def sample(utterance, bindings, k):
samples = list()
top_utterances = sorted(
bindings.keys(),
key=lambda u: dist(utterance, u),
)[:k]
for u in top_utterances:
for t in bindings[u]:
samples.append(t)
ts = local_sample(t, k)
samples.extend(ts)
return samplesExperiment
We built a bindings dataset (with about 44 labeled transformations) and ran the algorithm on different input utterances.
We used two different local-samplers: a neural network and a simpler ranking-based scheme.
def local_sample(transform, k):
local_sample = list()
# Ranking-based scheme
transforms = [RandomTransform() for _ in range(1000)]
transforms = sorted(
transforms,
key=lambda t2: dist(representative(transform), representative(t2))
)
local_sample.extend(transforms[:k//2])
# Neural network scheme
local_grammar_params = NN(t)
local_grammar = Grammar(grammar_params)
transforms = [local_grammar.sample() for _ in range(k)]
local_sample.extend(transforms[:k//2])
return local_sampleResults
Below you can interact with the data.
Legend:
The root-node has no meaning.
Each first-level node (i.e. each of the root children) is an input to the algorithm (“input nodes”).
The children of an input node represent the 10 most similar transformations in the dataset to the input node (“dataset nodes”).
The children of a dataset node represent transformations sampled from the neighborhood of the dataset node.
Appendix
Raw data of the results is attached in report.json
Raw data of the dataset is attached in bindings.json
The code is available at https://gitlab.com/da_doomer/program-by-talking/-/tree/representative-transforms.
