Incremental state machine manipulation
Last updated: Nov 18, 2021
Here I document how policies (functions that receive an observation and output an action) parametrized as state machines can be extended to acquire new skills. This is accomplished by exploiting the modularity of state machines through means of a Genetic Algorithm. We interpret our approach as joint optimization of a Domain Specific Language (DSL) and program synthesis in that DSL. Finally, we show that the proposed approach can synthesize state machines from scratch and extend them to acquire new skills in a locomotion task in two different environments. Furthermore, the individual components that generate the new behaviours can be identified and analyzed.
Introduction
It has been shown (Synthesizing Programmatic Policies That Inductively Generalize, 2020) that state machines can be used as robot controllers (“policies”): states get labeled with functions that map environment states to actions (“modes”), and edges are labeled with functions that output a scalar value (“switching conditions”). The action executed by the robot at any moment is the output of the active mode, and the switching condition with the biggest output determines the next active mode.
Programmatic State Machines are extremely well-suited to tackle the challenges of adapting to shifting environment conditions and acquiring new skills, as they are composed of discrete components that can be separately manipulated. As we show in this document, manipulation of pre-trained state machines through the addition of new modes and new switching conditions can extend the range of tasks at which the state machine successfully performs.
We focus on tasks where not many modes are needed, such as locomotion in different terrains. The work introducing Programmatic State Machines (Synthesizing Programmatic Policies that Inductively Generalize, 2019) showed that learning these policies directly is not easy, given that they have a combination of discrete and continuous parameters; so authors proposed a model-based optimization technique based on adaptive teaching. In this work we propose a model-free population-based algorithm that directly manipulates state machines for the optimization process.
State machines
We follow (Synthesizing Programmatic Policies That Inductively Generalize) and consider a Programmatic State Machine to be a tuple \((M, H, G, m_s, m_e)\) where
Modes \(m_i \in M\) are the memory of the state machine;
Each mode \(m_i\) corresponds to \(H_{m_i} \in H : S \to A\);
Each pair of modes \((m_i, m_j)\) corresponds to a switching condition \(G_{m_i}^{m_j}: S \to R\);
\(m_s\) and \(m_e\) are the start and end modes;
where \(S\) and \(A\) are respectively the environment state and action sets, so that the induced policy is defined by
\[\pi(o, s_n) = a_n\]
where
\(a_n = H_{s_n}(o_n)\)
\(s_{n+1} = \argmax_m G_{s_n}^m(o_n)\)
Note that a state machine can be interpreted as a program: modes correspond to “program primitives” and switching conditions correspond to flow-control statements.
Incremental state machine manipulation
Manipulation of a state machine \(\pi_\text{orig}\) induces a set of policies which we denote with \(<\pi_\text{orig}>\), that, when extending state machine \(\pi\) with new modes and switching conditions, is the set of state machines that have \(\pi\) as a sub-graph.
Thus, given a state machine \(\pi\) and a Markov Decision Process \((S,A,T,R,\gamma)\) (which may be different than the one used to optimize \(\pi\)) our objective is to find the manipulation of \(\pi\) that maximizes the expected value of the V-value function for a distribution \(S_0\) of initial states, so we aim to solve:
\[\pi^* = \argmax_{\pi \in <\pi_\text{orig}>}\mathbb{E}[\sum_{k=0} \gamma^kr_{t+k} | s_t \sim S_0]\]
where
\(r_t = \mathbb{E}_{a_t \sim \pi(\cdot | s_t)} R(s_t, a_t, s_{t+1})\) and
\(s_{t+1} \sim \mathbb{P}_\pi(\cdot | s_t, a_t)\)
Modes
On december 29, 2020 I wrote about representing modes as \(k\)-input parametric programs. Specifically, each program is a function \(f_i: R^k \to R^m\) with a corresponding input-building routine \(W_i: R^n \to R^k\) so that mode \(m_i\) is defined as:
\[H_{m_i}(o) = \operatorname{tanh}(f_i(\operatorname{tanh}(W_i(o))))\]
The parameters of a given mode are the union of the parameters of the program and the input-building function, so that
\[\theta_{H_{m_i}} = \theta_{f_i} \cup \theta_{W_i}\]
Functions of this form also have the added benefit of interpretability: as their input is restricted to a small amount of numbers, each restricted to a finite range through the \(\operatorname{tanh}\) function, one can “move a slider” in that range and observe all possible outputs.
In this work both the programs and the input-building routines are represented with linear functions, with the final modes taking the form of “bottle-neck” functions that reduce the observation dimensionality by forming arguments for an action program, as described above.
In our experiments we found that these “bottle-neck” functions perform as good as linear functions with the added benefit of increased interpretability. Neural Network functions perform at the cost of interpretability.
Switching conditions
As I wrote on december 28, 2020, a modular set of switching conditions is a set of hypervectors coupled with a global hyperdimensional encoder \(K\), so that
\[G_{m_i}^{m_j}(o) = \operatorname{sim}(K(o), v_{i,j}^K)\]
The parameters of a given switching condition are the values of each dimension of its representative hypervector, so that
\[\theta_{G_{m_i}^{m_j}} = v_{i, j}^f\]
In this work we use cosine similarity as the similarity metric.
Optimization
Note that the union of the modes of individuals in a population of state machines forms a set of “program primitives”. Each individual is then a program (defined by its switching conditions) that uses some of these primitives. The programs and the primitives are jointly optimized by means of a Genetic Algorithm. The programs do not evolve in isolation, as the algorithm combines the components of different programs. We interpret this algorithm as joint design of a Domain Specific Language (DSL) and program synthesis in that DSL.

Population of state machines as programs in an evolving DSL. Outlines are changed to denote mutated modes.
Optimization takes place by modifying a set of “mutable” modes and switching conditions. When extending a state machine the set of mutable modes and switching conditions includes only the new states and switching conditions (i.e. when extending we “freeze” the original state machine). Optimizing an initial state machine is the special case of extending the empty state machine.
Algorithm
In particular, we propose optimizing the state machines and their extensions with a population-based gradient-free optimization process. The overall process of extending a state machine is divided into two phases:
Optimization of initial state machine \(\pi_\text{orig}\) in an environment.
Optimization of the optimal extension in \(<\pi_\text{orig}>\) in a different environment.
Both optimization phases are carried out by a Genetic Algorithm which performs the following steps:
Population initialization: initialize set of programs with different primitives.
Fitness evaluation: evaluate the fitness of each program.
Elitism: select the best programs.
Mode mutation: mutation of the primitives in the current DSL.
Switching condition mutation: mutation of the programs in the library.
Crossover: use primitives of one program in another.
You can see a summary of this procedure in the code below:
function optimize(
statemachine_init,
generations,
fitness,
mutation_routine,
crossover_routine,
elite_number,
mutated_number,
crossover_number,
)
# Initialize population
population_size = mutated_number + crossover_number
population = [statemachine_init() for _ in 1:population_size]
for _ in 1:generations
# Select elites
population_fitness = map(fitness, population)
sorted_population = population[sortperm(population_fitness)]
elites = take(sorted_population, elite_number)
elite = first(elites)
# Mutate elites
mutated_elites = map(mutation_routine, rand(elites, mutated_number))
# Crossover elites
crossover_elites = map(crossover_routine, rand(elites, crossover_number, 2))
end
elite
endOperators
We now define the operators employed in the Genetic Algorithm.
Fitness
The fitness function chooses randomly an environment on which to execute and evaluate the given state machine.
During optimization, we further exploit the population-based nature of the proposed optimization process by treating the values of out-edges of a mode (given by switching conditions) as the probabilities of a categorical distribution, which we sample from to choose the next active mode, instead of choosing it deterministically with the largest value. This “softening” of the discrete transitions allows us to identify state machines whose transitions are closer to the correct outputs.
(in principle this should not be needed, given the design of the switching conditions. but experiments will tell if it boosts performance) During extension the state machines are evaluated on both the new and the original environments. This allows to optimize new switching conditions so that they activate exactly when they should activate. Specifically, the fitness function iterates through a list of active environments at least once.
Mutation
The mutation operator for parameter vectors is defined as
\[\operatorname{mutate}(\theta) = \theta + \epsilon\sigma\]
where \(\epsilon \sim N(0, 1)\) and \(\sigma \in R\) is a hyperparameter. Empirically we found that \(\sigma = 0.00001\) for switching conditions and \(\sigma = 0.1\) for modes yield good results.
The mutation operator is applied to all mutable modes and switching conditions.
We bias the optimization process to yield “small programs” by removing or adding switching conditions during mutation, with probabilities \(p_\text{remove}\) and \(p_\text{add}\). We set this probability so that it is more likely to remove switching conditions from very dense graphs than from sparse graphs: \(p_\text{remove} = \frac{|E|}{|E_m|}\) and \(p_\text{add} = 1-p_\text{remove}\), where \(E_m\) is the set of mutable edges and \(E \subseteq E_m\) is the set of active mutable edges.
Crossover
Crossover corresponds to forming new programs with primitives drawn from the DSL of the set of modes of the current elites.
To form new programs the primitives are arranged in a way that mimics the current arrangements: transitions to new primitives are drawn from current programs.
Specifically, we form \(\pi_3\), the crossover of \(\pi_1\) with \(\pi_2\) as follows:
Copy \(\pi_2\) into a new state machine \(\pi_3\)
Choose a mode \(m_1 \in \pi_1\) and a mutable mode \(m_2 \in \pi_2\).
Replace \(m_2\) with \(m_1\) in \(\pi_3\).
Optionally replace the transitions to the newly placed mode in \(\pi_3\) with transitions that went to \(m_1\) in \(\pi_1\).
Thus, the crossover operator is defined as follows:
function crossover(s1::StateMachine, s2::StateMachine)
s3 = deepcopy(s2)
if length(s3.mutable_states) == 0
return s3
end
# Select a state in s1
i1 = rand(1:s1.state_number)
# Select a mutable state
i2 = rand(s3.mutable_states)
# Copy the state to the mutable state
s3.states[i2] = deepcopy(s1.states[i1])
# Copy some transitions
for j2 ∈ 1:s3.state_number
replace_transition = rand([true, false])
if replace_transition
s3.transitions[j2, i2] = deepcopy(rand(s1.transitions[:,i1]))
end
end
s3
endNote that crossover of modes allows new modes to be be variations of pre-existing modes. These “copied” modes benefit in turn from crossover of switching conditions, as the copied switching conditions can be mutated to activate at exactly the right time.
Initialization

Example execution of the initialization routine, extending a state machine with a single mode.
Let \(\pi_\text{orig} = (M, H, G, m_s, m_e)\) be a state machine. The initialization routine for a state machine in \(<\pi_\text{orig}>\) with \(k\) new modes is defined as follows:
\[\operatorname{extend}(\pi_\text{orig}, k) = (M', H', G', m_s, m_e)\]
where
\(M' = M \cup \{m_i'\}_{i=1}^{i=k}\);
\(H' = H \cup \{H_{m_i'}\}_{i=1}^{i=k}\) with parameters \({\theta}_{H_{{m_i}'}} \sim N(0,1)\).
\(G' = G \cup \{G_{m_i'}^{m_j'}\} \cup \{G_{m_i'}^{m_i} | m_i \in \pi_\text{orig}\} \cup \{G_{m_i}^{m_i'} | m_i \in \pi_\text{orig}\}\) for \(1 \leq i,j \leq k\) with parameters \({\theta}_{G_{m_1}^{m_2}} \sim N(0,1)\) for every new switching condition \(G_{m_1}^{m_2} \in G' - G\) (i.e. new switching conditions for every new pair of modes and from and to every original mode).
The initialization routine also marks the new modes and new transitions as the only “mutable” structures.
Related work
In (Synthesizing Programmatic Policies that Inductively Generalize, 2020) authors propose a framework for optimize state machines in which optimization alternates between updating a teacher, which is an overparametrized version of the student, and the student, which is trained to mimic the teacher.
In (Reinforcement Learning with Competitive Ensembles of Information-Constrained primitives, 2019) authors optimize a memory-less policy composed of a set primitives that “activate” through an information-theoretic mechanism.
In (Blind Hexapod Locomotion in Complex Terrain with Gait Adaptation Using Deep Reinforcement Learning and Classification, 2019) a multiplexing architecture for terrain composed of discrete terrain distributions is proposed. First, a policy is trained for each of the terrains using reinforcement learning and then a terrain classifier is trained by sampling rollouts on compound terrains.
In (Composing Task-Agnostic Policies with Deep Reinforcement Learning, 2020) authors propose an architecture that weights the output of primitive policies to solve new tasks. The primitive policy weights are computed at each environment state through an LSTM encoder-decoder network that feeds an attention module.
In (Multi-expert learning ofadaptive legged locomotion, 2020) a Gating Neural Network architecture that combines multiple expert Neural Networks to synthesize a policy in an on-line fashion is proposed.
In (Incremental Hierarchical Reinforcement Learning With Multitask LMDPs, 2019) a scheme to infer hierarchical structures of multi-task Linearly-solvable Markov decision processes is extended to develop an agent capable of incrementally growing a hierarchical representation used to improve exploration.
In (Paired Open-Ended Trailblazer (POET): Endlessly Generating Increasingly Complex and Diverse Learning Environments and Their Solutions, 2019) authors propose optimizing the behavioural optimization in a population of policies evolved through Evolution Strategies. The test is also on the BipedalWalker environment.
Results
Experiments are still ongoing. You can see preliminary results in the december 28 and december 29 posts.
Example evolution of the elite fitness values during optimization on BipedalWalker-v3.
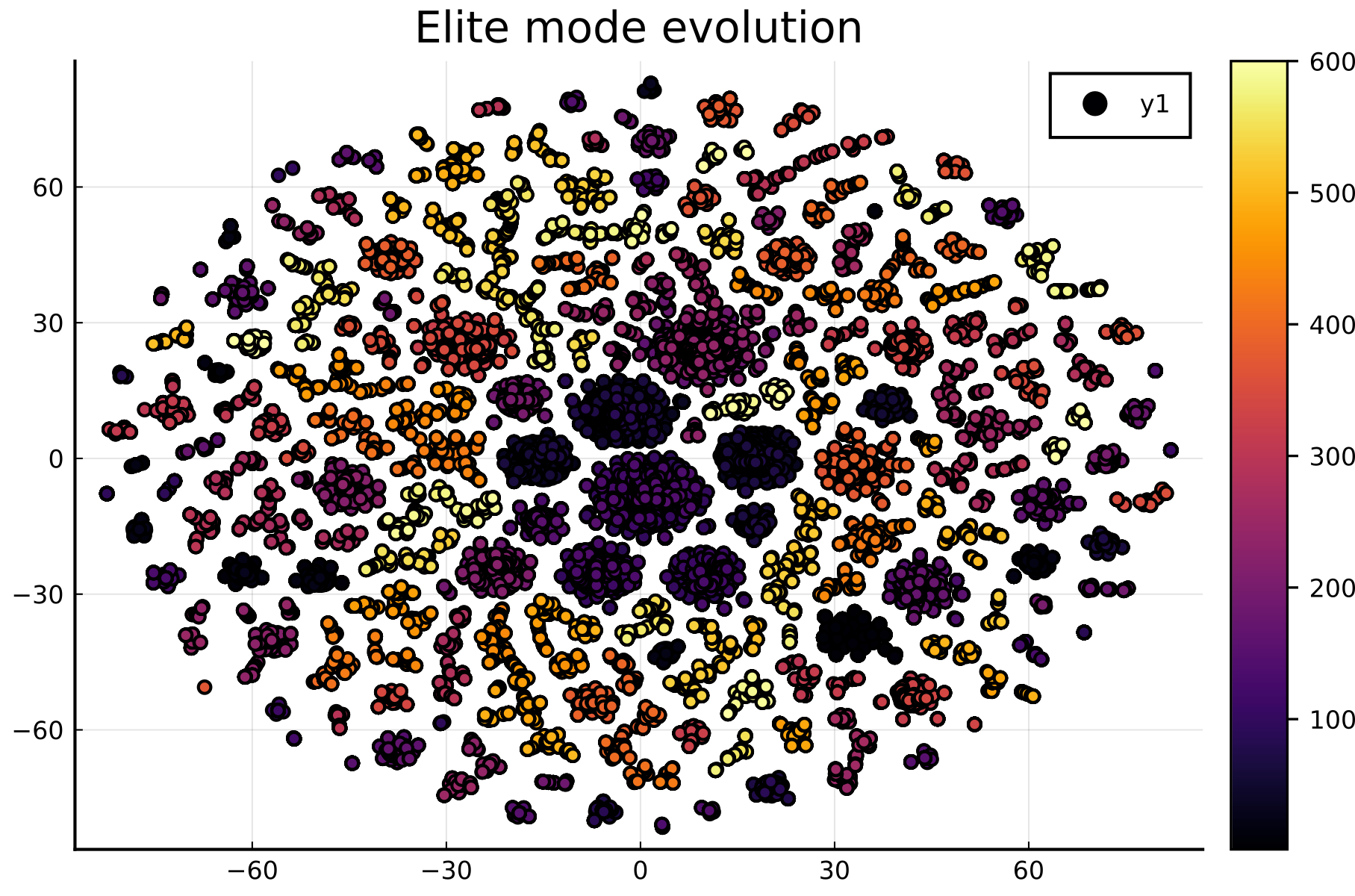
Example evolution of the elite modes in the population during optimization on BipedalWalker-v3. after applying the TSNE algorithm. Each circle is a primitive in the evolving DSL. Color encodes to which generation each primitive belongs.
Conclusion
(preliminary results point to this being the conclusion of our experiments, but experiments are still ongoing)
We have proposed a population-based algorithm for extending state machines. The algorithm can synthesize policies from scratch by “extending” the empty state machine. The proposed algorithm is simple to implement and does not require access to gradients.
We tested our algorithm in simulation on the locomotion task on a simple “mostly flat” terrain. Results showed that the proposed algorithm succesfully optimizes state machines.
In future work we plan to further exploit the modular and programmatic aspects of state machines for joint optimization of robot controllers and robot design. Population-based optimization of state machines also opens the door to non-reward-function optimization of state machines (e.g. optimizing diversity) and multi-agent optimization.
